Seminario 5: Exposición de las Investigaciones.

Este seminario ha sido el día que todos esperábamos nerviosos y con miedo, ya que se trataba de nuestro primer proyecto de investigación y las dudas nos asaltaban a cada paso. Ha sido un gran alivio ver que todos los proyectos iban dando un resultado tan bueno, es una alegría que a todos los grupos de mi seminario les saliese una trabajo tan bueno. Entre los temas que se han tratado han estado la alimentación en niños-adolescentes, la eutanasia, el aborto, y por último nuestro proyecto que traba sobre las conductas de machismo benevolente entre los jóvenes de entre 16 y 18 años.
Personalmente, estoy muy orgullosa de nuestro proyecto, ya que nos supuso un gran esfuerzo, y muchas horas de trabajo, pero ha merecido la pena ya que todo esfuerzo da su fruto.

Seminario 4:

En este Seminario hemos vuelto a tratar el programa EpiInfo, ya que una vez obtenidas las gráficas, tablas y demás operaciones estadísticas nos quedaba la aparentemente fácil tarea de interpretarlos lo cual no fue tan fácil como esperábamos no obstante, ha sido una tarea asequible para todos. Hemos podido avanzar en este sentido en los proyectos con nuestros respectivos grupos, lo que nos ha permitido preguntar dudas sobre nuestros proyectos al tiempo que íbamos interpretando los resultados de nuestros trabajos.

En este seminario hemos vuelto ha resolver dudas ya que al avanzar más los conocimientos que debemos adquirir son más difíciles lo que crea aún más confusión entre nosotros.

Seminario 3

En el tercer seminario que tuvimos empleamos la primera mitad de la clase en resolver dudas, ya que en esta asignatura es fácil que surjan errores de compresión, ya que no sólo se trata de aprenderse un temario de memoria , hay que saber aplicarlo en los diferentes problemas que se nos proponen, también estuvimos adelantando conceptos con la idea de que la próxima clase teórica fuese más comprensible para todos.

La segunda mitad de la clase continuamos con nuestro aprendizaje sobre el programa EpiInfo, como ya habíamos aprendido en el Seminario 2 a crear un cuestionario e introducir los datos en él, esta vez nos centramos en las operaciones estadísticas que debíamos realizar para así obtener los resultados en nuestros respectivos trabajos. Vimos diferentes métodos que se podía usar como las tablas de frecuencia o los gráficos, que a la hora de exponer nuestro trabajo son muy útiles ya que son claros y fáciles de comprender. 

Gracias a este seminario hemos podido dar un pasito más en nuestros proyectos, acercándonos cada vez más al final

10. Hipótesis estadísticas. Test de hipótesis:

En esta entrada veremos cómo comprobar que la hipótesis hecha para un estudio es aceptada o no lo es. Además de los intervalos de confianza existen otros métodos para controlar los errores, éstos serán los test de hipótesis.
Primero deberemos establecer una hipótesis sobre el valor del parámetro, después realizaremos la recogida de datos, y por último analizaremos la coherencia entre la hipótesis y los resultados que hemos obtenido.
El test de hipótesis se contratará con la hipótesis nula. Nos centraremos en el test que relaciona variables cualitativas con variables cualitativas, éste será Chi-cuadrado.

Test de hipótesis Chi-cuadrado:

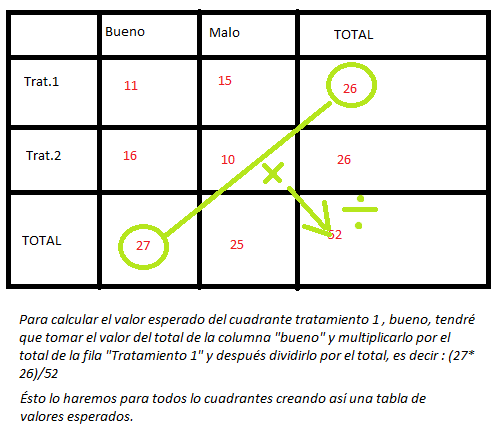
Para calcularlas se nos dará una tabla con los datos obtenidos, nosotros tendremos que crear una tabla con los datos esperados para ello.:

Una vez hecha la tabla de valores esperado aplicamos la siguiente fórmula:

A continuación tenemos que calcular el grado de libertad de la tabla, para ello multiplicaremos el número de final -1 (sin contar la fila de TOTAL) , por el número de columnas -1 (sin contar con la columna TOTAL). En esta tabla nos daría 1. El grado de libertad se buscará en la tabla de Chi-cuadrado para el valor 0.05.
-Si el valor que me da la tabla es mayor que el de Chi-cuadrado aceptaremos la Hipótesis nula.
-Si el valor que me da la tabla es menor que el de Chi-cuadrado rechazaremos la Hipótesis nula.

Errores de hipótesis:

• Error tipo 1 o error alfa: Se tratará del error que cometemos si rechazamos la hipótesis nula cuando en realidad era cierta.
• Error tipo 2 o error beta: Se trata del error que cometemos al aceptar la hipótesis nula siendo ésta falsa.

Tendrá gran importancia realizar test de hipótesis a nuestras investigaciones, ya que no siempre serán ciertas nuestras hipótesis por lo que tendremos que comprobar si realmente lo son o no.

9. Estadística inferencial. Muestreo y estimación:

 Comenzaremos esta entrada definiendo algunos término necesarios:

• Población de estudio: Será el conjunto de pacientes sobre el que queremos estudiar alguna cuestión.
• Muestra: Son el conjunto de individuos que participan en el muestreo.
• Tamaño muestral: Es el número de individuos que forman la muestra.
• Inferencia estadística: Son los procedimientos estadísticos que nos permitirán pasar de lo particular, la muestra, a lo general, que es la población.
• Técnica de muestreo: Son los procedimientos que nos permiten elegir muestras de forma adecuada, es decir que reflejen las características de la población.
• Muestreo probabilístico o aleatorio: Es la muestra elegida por un proceso al azar.
• Error aleatorio: Es el erro que irá asociado a la muestra que ha sido elegida mediante un proceso de azar.

Proceso de la inferencia estadística:

Se hace una selección aleatoria de una población de estudio y de ahí se obtiene la muestra, la medida de la variable de estudio que hemos obtenido será el estimador, a partir del estimador, mediante un proceso llamado inferencia, me acercaré al parámetro, que será la variable que queremos medir en la población.



Error estándar:

Se trata de una medida cuya función es mostrar la variabilidad de los valores del estimador, que será la media o una proporción. Mientras menor sea este error estándar más fiable será el valor de nuestra muestra. Se calcula de la siguiente manera:

-Para una media:                                                      -Para una proporción:

Intervalos de confianza:
Los utilizaremos para conocer el parámetro en una población , midiendo el error aleatorio. Nos dará dos números, con un nivel de confianza determinado, dentro de los cuales podemos decir que se encuentra el x% de nuestra población. La formula será:
- I.C. de un parámetro=estimador+/- Z*(e. éstándar)

Técnicas de muestreo: 

Un muestreo es un método por el cual podremos coger un grupo pequeño de una población, teniendo un grado de probabilidad de que este grupo posea las características de la población que estamos estudiando.
Tipos de muestreo:

-Muestreo Probabilístico: Todos los elementos tendrán la misma probabilidad de ser elegidos.

• Aleatorio simple:Cada unidad tiene una probabilidad equitativa de ser incluida en la muestra. Podrá ser de sorteo,el cual no podrá aplicarse a poblaciones muy grandes o por una tabla de número aleatorios.
• Aleatorio sistemático:Será parecido al simple, todos los individuos tendrán la misma posibilidad de ser selccionados. Las elegiré ordenándolas y escogiéndolas mediante un intervalo, ej: 10,20, 30,40...
• Estratificado:Se subdivirá la población en estratos, debido a que las variables deberán someterse a estudio.
• Conglomerado:En la selección en lugar de escoger una unidad se escogerán grupos o conglomerados.

-Muestreo no Probabilístico: Será aquel que no sigue el proceso aleatorio.

• Por cuotas: El investigador seleccionará la muestra teniendo en cuenta algunos fenómenos o variables a estudiar.
• Accidental:Se utilizará a las personas disponibles en un momento dado, según lo que interese estudiar.

Tamaño de la muestra:

Será el número mínimo de individuos que necesitamos en la muestra para realizar la investigación. Éste dependerá del error estándar, de la variabilidad de la variable a estudiar, del tamaño de la población...  su formula será:

Tras calcular el tamaño de la muestra habrá que comprobar si es el valor correcto mediante:

-  N> n*(n-1) Si no se cumple habrá que calcular n mediante el cálculo de n´:

-n´= n/1+ (n/N)

Sin embargo cuando queramos calcular el tamaño de una muestra cuando queremos estimar una proporción usaremos la siguiente fórmula:

8. Medidas de tendencia central, posición y dispersión:

En esta entrada veremos diferentes maneras de interpretar los datos, así como ver que tipo de distribución tienen y las asimetrías y curtosis que pueden presentar.

Resumen numérico de una serie estadística:
Nuestras observaciones también podremos resumirlas mediante datos estadísticos. Las medidas estadísticas pueden dividirse en:

-Medidas de tendencia central: Nos darán una idea del tamaño de los datos.

• Media aritmética o media: Se usará para variables cuantitativas. Es la suma de todos los valores del variable entre el número total de observaciones. Nos mostrarán en centro geométrico de los datos. Si los datos están agrupados sumaremos los intervalos de clase multiplicados por su frecuencia absoluta correspondiente y lo dividiremos entre el número de observaciones.
• Mediana: Será el valor que, si colocamos todas las variables en escala de menor a mayor, deje el 50% de las observaciones por encima, y el 50% de las observaciones por debajo. Si el número de observaciones es impar la mediana será justamente el número que se encuentra en las posición (n/2+1). Por el contrario si el número de observaciones es impar, será la media de los dos valores centrales.
• Moda: Es el valor que más se repite en nuestras observaciones. SI hay dos valores que se repiten el mismo número de veces será bimodal, y si son más de dos los que se repiten el mismo número de veces se llamará multimodal. Si los datos están agrupados y la amplitud es la misma en todos los intervalos la moda se encontrará en el intervalo cuya frecuencia absoluta sea mayor. SI la amplitud entre los intervalos es diferente la moda se encontrará en el intervalo en el que el cociente entre la frecuencia relativa y la amplitud sea mayor. 

-Medidas de posición: Se usan para variables cuantitativas, sólo se tendrá en cuenta la posición de los valores de la muestra.

• Percentiles: Dividirán la muestra en 100. El percentil i será aquella que, ordenadas todas las observaciones de la muestra, el i% de las observaciones sean menores y el 100-i% sean mayores.
• Deciles: Se dividirá la muestra en 10 partes el decil i será aquel que, ordenando las muestras de menor a mayor, el i/10% sean menores que el y el (100-i)/10% sean mayores.
• Cuartiles: Dividirán la muestra en cuatro partes, el Q1 por ejemplo indicará que el 25% de las observaciones son menores que el y el 75% mayores.

-Medidas de dispersión: 

• Rango o recorrido: Será la resta del valor mayor de la muestra y el menor. Mientras mayor sea el recorrido más dispersión habrá.
• Desviación media: Será la media aritmética de las distancias de cada observación con respecto a la media de la muestra.
• Desviación típica: Nos mostrará el margen de error que cometeríamos si representásemos una muestra solo por su media.

          

• Varianza: Expresará la misma información que la desviación media pero elevada al cuadrado.
• Recorrido intercuatílico: Será el valor absoluto de la diferencia entre el tercer y el primer cuartil.
• Coeficiente de variación: Es una medida de dispersión relativa adimensional, compararemos la heterogeneidad de dos series numéricas. Será la división de la desviación típica entre la media aritmética.

Distribuciones normales:

Será la distribución de Gauss es una de las distribuciones de probabilidad de variable continua que aparece con más frecuencia en los fenómenos reales.
Se trata de una gráfica con forma de campa y simétrica con respecto a los valores de posición central.

Asimetrías y curtosis:

Las simetrías pueden ser:

• g1=0 Querrá decir que se trata de una distribución simétrica, habrá la misma concentración de valores a la izquierda y a la derecha.
• g>0: Se trata de una distribución asimétrica positiva, habrá mayor concentración a la derecha de la media.
• g<0: Se trata de una distribución asimétrica negativa, en ella habrá mayor concentración de valores a la izquierda de la media.

Los tipos de curtosis son:

• g2=0 Será una distribución mesocúrtica. EL grado de concentración medio está alrededor de los valores centrales de la variable.
• g2>0 Será una distribución leptocúrtica, ésta presentará un  gran grado de concentración en torno a los valores centrales de la variable.
• g2<0 Distribución platicúrtica, habrá un reducido grado de concentración en torno a los valores centrales de la variable.

7. Introducción a la Bioestadística:

En esta entrada se hablará de qué es la estadística y como es aplicada al ámbito de la salud.
La estadística es la ciencia que estudia la variabilidad. Nosotros la usaremos por ejemplo, para relacionar algún factor de riesgo con una enfermedad, por ejemplo el tabaco con padecer una EPOC.

Escalas para medir las variables:

• Escala nominal: Se trata del nivel inferior de la medida en ella sólo podremos comprobar si las variables son iguales o diferentes, es decir, no podremos dar categorías a las variables ni podremos agruparlas, por ejemplo el sexo:  Hombre/Mujer.  Las categorías serán excluyentes, si se pertenece a un grupo no se podrá pertenecer al otro.                                                          
•  Escala ordinaria: Se dan varias modalidades de una variable, en ellas se podrá establecer si son iguales o diferentes y en el caso en el que sean distintas se podrá determinar cual de ellas es mayor. Ejemplo: El grado de acuerdo con respecto a algunas afirmaciones. Esta escala sólo establece un orden/categoría.
•  Escala de medida. Escala de intervalo: En ellas se presenta identidad y orden, los intervalos de esta escala serán iguales, pero no se podrán obtener proporciones. Al ser una escala cuantitativa, se podrá aplicar la estadística. Un ejemplo sería la temperatura corporal.
• Escalas de medida. Escalas de razón:  Es el nivel más alto de medición, tendrá las características de las tres escalas anteriores. Tendrá identidad, orden, distancias equivalentes entre los intervalos y además poseerá el 0 absoluto , como por ejemplo el peso la altura, el número de enfermos de un hospital...

 Tipos de variables:

• Cualitativas: Serán propiedades que no pueden ser medidas, de dividirán en dicotómicas (se dividen en dos niveles o categorías) o policotómicas (se dividirán en más de dos categorías).
• Cuantitativas: Éstas se podrán medir de forma numérica podrán ser discretas (únicamente podrán tomar números finitos que además no podrán ser fraccionados, como el número de hijos) o continuas( éstas podrán valer cualquier número dentro de un rango, como la talla)

Representaciones gráficas:Será la forma más rápida de comunicar la información, son muy útiles para ofrecer una orientación sobre lo que estamos hablando. Las representaciones gráficas deben de ser:
-Claras.
-Deben describirse en el pie de la gráfica y en el texto.
-Deben representar las conclusiones del estudio.
- Se debe evitar gráfico muy recargados ya que impedirán su compresión.

• Gráfico de barras: Servirán para variables cuantitativas discretas. No servirán para variables continuas.
• Histogramas y polígonos de frecuencia: Se usa para variables continuas, si la amplitud del intervalo es igual solo habrá que elevar las columnas, en cambio, si la amplitud de los intervalos es diferentes el ancho de la barra deberá mostrar esa amplitud.

• Gráfico de troncos y hojas: Nos mostrará la forma en la que se hace la distribución y los valores que tomará la variable. En el tronco se pondrán las decenas y las unidades al lado de cada decena correspondiente, éstas serán las hojas.
• Gráficos para datos bidimensionales: En estas gráficas podremos relacionar tres tipos de variables.

6. La etapa empírica de la investigación: El diseño, el material y los métodos.

En esta entrada continuaremos viendo cómo desarrollar nuestra investigación, será muy importante determinar el diseño de la investigación , ya que no será lo mismo un estudio descriptivo que uno experimental.

Material y métodos:

• Habrá que seleccionar la población sobre la que queremos estudiar, si se trata de una población muy grande tendremos que seleccionar una muestra. Para no superar un error determinado (normalmente del 5%) habrá que calcular el tamaño de nuestra muestra.
• Habrá que planificar el modo en el que se recogerán los datos,para así buscar la relación entre las dos variables de nuestra investigación.  Podremos recogerlos por observación directa, a través de entrevistas, cuestionarios, formularios...
• Una vez obtenidos los datos habrá que agruparlos y distribuirlos según una frecuencia, construir una tabla, usar bases de datos...
• Análisis, habrá que revisar la información obtenida, y aplicarle técnicas de estadísticas, para compararlas, controlar las variables, estimar el grado de asociación, detectar errores y definir su validez.

Diseños cuantitativos:

• Diseño descriptivo: Se estudia en un momento concreto dos variables, el investigador no introduce variables, sólo analiza. En este tipo de estudios mediremos la prevalencia con ella describiremos la proporción de la población que presenta la enfermedad (o lo que estemos midiendo) en un punto específico del tiempo.

• Diseño analítico: 

           -Estudio de cohortes o de seguimiento: Se medirá la asociación entre dos fenómenos haciendo un seguimiento en el tiempo (PROSPECTIVO) para analizar como una variable afecta a la enfermedad. O se les hará un estudio sobre si cumplían la variable o no en el pasado y ver como afecta en el presente. En este tipo de estudios mediremos la incidencia que  nos dará la información de lo que ha pasado durante un tiempo determinado, por ejemplo, cuantos han enfermado en un año, entre quienes estaban expuestos a un factor de riesgo y quienes no lo estaban. Para calcular la incidencia usaremos el riesgo relativo.

-Estudio de casos y controles: Tomamos una muestra que padezca la enfermedad y buscamos las causas de ella, para ver si la variable se encuentra entre las causas, tomaremos otra muestra que no padezca la enfermedad y haremos los mismo. Con este tipo de investigación pretendemos ver la relación que hay entre la variable (o factor de riesgo) y padecer la enfermedad. Para medir esta asociación usaremos la ODDS RATIO.

Diseño experimental: Mediremos la fuerza de asociación entre dos fenómenos, pero la variable independiente será introducida por el investigador, y él mismo formulará una hipótesis con el resultado que espera obtener. En este tipo de diseño habrá que tener cuidado ya que puede presentar problemas éticos. En este tipo de diseño también usaremos la Incidencia para medir la asociación entre las variables y la enfermedad.